数据的图表展示
数据的预处理
数据的预处理是在对数据分类或分组之前所做的必要处理,内容包括数据的审核、筛选、排序等。
数据审核
数据审核就是检查数据是否有错误。
对于通过调查取得的原始数据,主要从完整性和准确性两个方面去审核。
- 完整性审核:检查应调查的单位或个体是否有遗漏,所有的调查项目是否填写齐全等。
- 准确性审核:检查数据是否有错误,是否存在异常值。(保留还是纠正)
对于其他渠道取到的二手数据,应着重审核数据的适用性和时效性。
数据的展示
分类数据和顺序数据统称为品质数据
数据经过预处理后,可根据需要进一步做分类或分组。对品质数据主要是做分类整理,对数值型数据则主要是做分组整理。
频数:落在某一特定类别或组中的数据个数
频数分布:把各个类别及落在其中的相应频数全部列出,并用表格形式表现出来。
列联表:由两个或两个以上变量交叉分类的频数分布表也称为列联表。
比例:也称构成比,它是一个样本(或总体)中各个部分的数据与全部数据之比,通常用于反映样本(或总体)的构成或结构。
百分比:将比例乘以100得到的数值称为百分比
比率:样本(或总体)中不同类别数据之间的比值,由于比率不是部分或整体之间的对比关系。
| 图形 | 分类数据 | 顺序数据 | 数值型数据 |
|---|---|---|---|
| 频数分布 | 除了频数,还可以给出相应的百分比,有效百分比,累计百分比等。 由于不存在缺失值,表中的百分比和缺失百分比完全相同 频数分布表 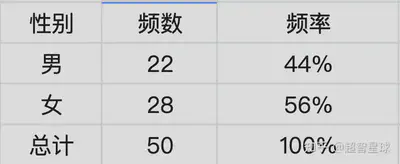 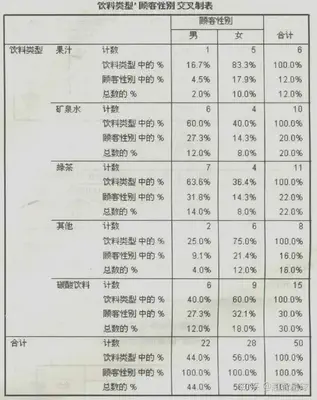 |
跟分类数据类似,只不过类别有顺序 | 先分组,然后计算各个组的频数或频率 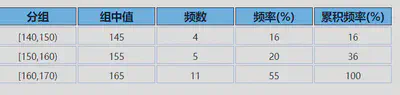 |
| 累计频数分布 | 累计频数:将各有序类别或组的频数逐级累加起来得到的频数 向上累积:从类别顺序开始的一方向类别顺序的最后一方累加频数 向下累积:从类别顺序的最后一方向类别顺序的开始一方累加频数 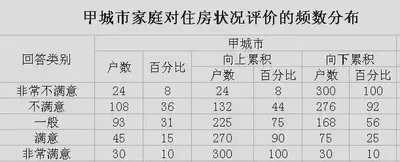 |
向上累积:从变量值小的一方 向 变量值大的一方累加频数 向下累积:从变量值大的一方 向 变量值小的一方累加频数 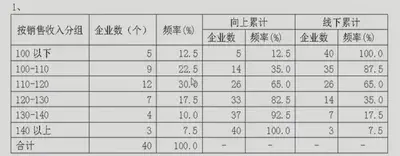 |
|
| 累积分布图 |
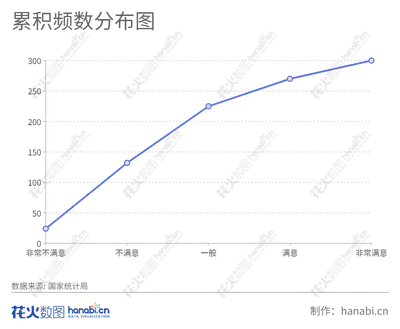 |
  |
|
| 条形图 | 用宽度相同的条形的高度或长短来表示数据多少的图形。 可以横置或纵置,纵置时也称为柱状图 还有简单条形图和复式条形图等形式 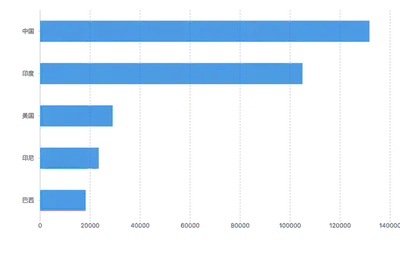 |
差不多 | 先分组,然后绘制,其实应该叫做直方图了 |
| 帕累托图 | 按照类别数据出现的频数多少排序后绘制的条形图
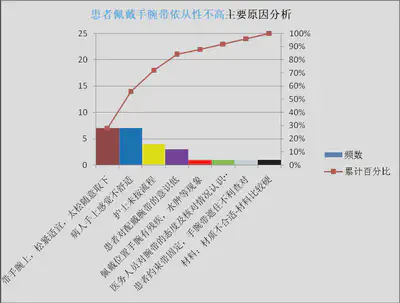 |
类别换成顺序数据即可 | 同理直方图+累积频数 |
| 饼图 | 用圆形及圆内扇形的角度来表示数值大小的图形,它主要用于表示一个样本(或总体)中各组成部分的数据占全部部分的比例,对于研究结构性问题十分有用
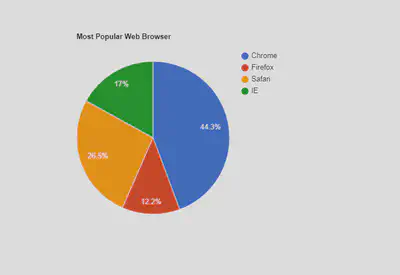 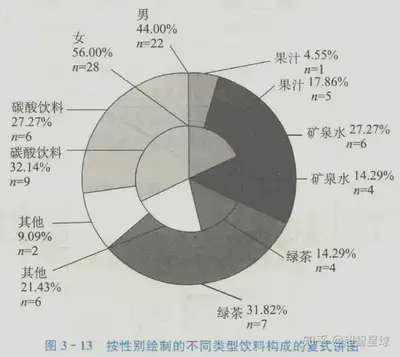 |
类别换成顺序数据即可 | 分组,然后绘制 |
| 环形图 | 如果有两个总体或两个样本的分类相同且问题可比,可以绘制环形图.环形图可显示多个样本各部分所占的相应比例
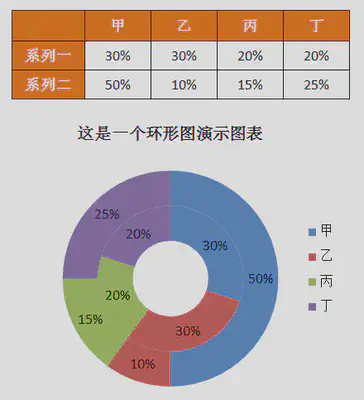 |
换成顺序数据 | 分组绘制 |
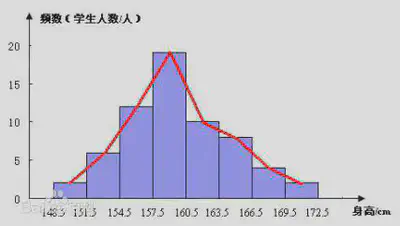
| 直方图 | 显示分组数据分布特征的图形有直方图、折线图和曲线图等。 直方图:展示分组数据分布的一种图形,它是用矩形的宽度和高度(即面积)来表示频数分布的。 直方图与条形图的区别: 1. 条形图是用条形的长度(横置时)表示各类别频数的多少,其宽度则是固定的,直方图是用面积表示各组频数的多少,矩形的高度每一组的频数或频率,宽度则表示各组的组距,因此其高度与宽度均有意义 2. 由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列 3. 条形图主要用于展示分类数据,而直方图则主要用于展示数值型数据. 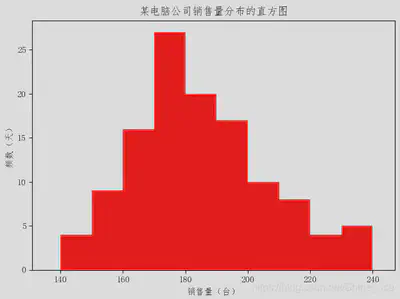 |
||
| 茎叶图 | 茎叶图是反映原始数据分布的图形。通过茎叶图,可以看出数据的分布状况及离散状况,比如,分布是否对称,数据是否集中,是否有离群点。 茎叶图的绘制:一般叶上保留最后一位,很大的数可以保留两位,数字之间用逗号分隔。 茎叶图与直方图的比较: 1. 茎叶图类似于横置的直方图,与直方图相比,茎叶图既能给出数据的分布状况,又能给出每一个原始数值,即保留的原始信息。 2. 直方图通常适用于大批量数据,而茎叶图通常适用于小批量数据(个数较少且数据相对集中)  |
||
| 箱线图 | 根据一组数据的最大值、最小值、中位数、两个四位数这五个特征值绘制而成的。它主要用于原始数据分布的特征,还可以进行多组数据分布特征的描述。
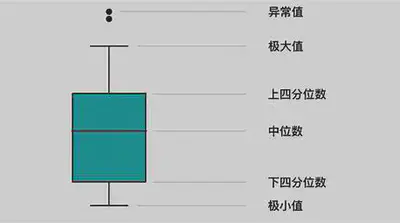 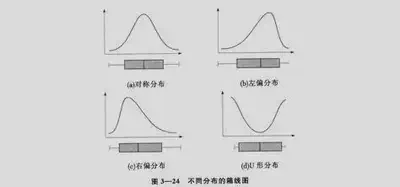 |
||
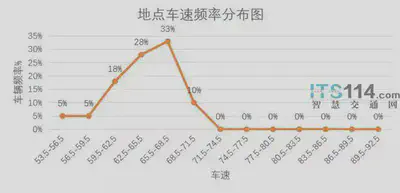
| 线图 | 线图主要用于反映现象随时间变化的特征。
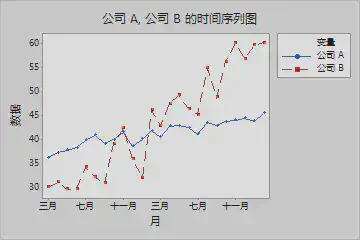 |
||
| 散点图 | 散点图是用二维坐标展示两个变量之间关系的一种图形。
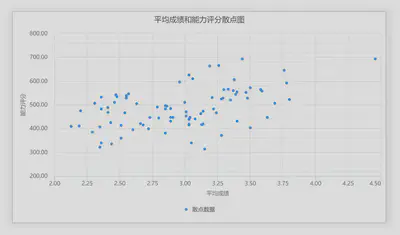 |
||
| 气泡图 | 气泡图可用于展示三个变量之间的关系。一个变量放在横轴,一个变量放在纵轴,第三个变量则用气泡的大小来表示。
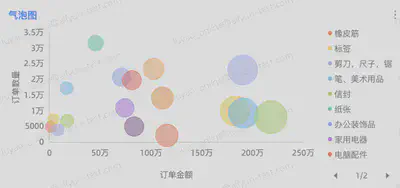 |
||
| 雷达图 | 由n个样本形成的n个多边形就是一张雷达图。 雷达图在显示或对比各变量的数值总和时十分有用。假定各变量的取值具有相同的正负号,则总的绝对值与图形所围成的区域成正比。此外,利用雷达图还可以研究多个样本之间的相似程度。 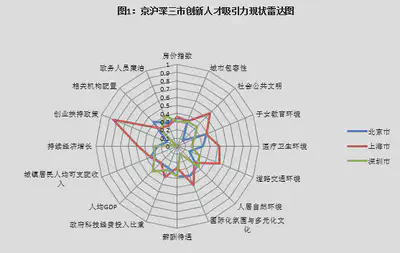 |
数值型数据的频率分布图
将原始数据哪找某种标准分成不同的组别,分别后的数据称为分组数据,数据分组的主要目的是观察数据的分布特征。
数据分组的方法:
- 单变量值分组:把每一个变量值作为一组,通常只适合离散变量,且在变量值较少的情况下使用。
- 组距分组:在连续变量或变量值较多的情况下。将全部变量值依次划分为若干个区间,并将一个区间的变量值作为一组。在组距分组种,一个组的最小值称为下限,一个组的最大值称为上限
频数分布表的编制过程:
- 确定组数
一般情况下,一组数据所分的组数不应少于5组且不多于15组,即
- 确定各组的组距
组中值
- 每一组中上限值与下限值中间的值,即
- 使用组中值代表一组数据的必要前提条件:各组数据在本组内呈均匀分布或在组中值两侧呈对称分布。
- 每一组中上限值与下限值中间的值,即
开口组,闭口组
如果全部数据中的最大值与最小值和其他数据相差悬殊,为避免出现空白组(即没有变量值的组)或个别极端值被漏掉,第一组和最后一组可以采取
等距分组和不等距分组
- 组距相等还是不相等
- 根据分组编制频数分布表。
- 原则:不重不漏.不重是指一项数据只能分在其中的某一组,不能在其他组中重复出现;不漏是指组别能够穷尽,即在所分的全部组别中每项数据都能分在其中的一组,不能遗漏。
- 不重:习惯上规定:上组限不在内。,当然,对于离散型变量,可以采用相邻两组组限间断的方法解决不重的问题。对于连续变量,可以采取相邻两组组限重叠的方法,根据“上组限不在内”的规定解决不重的问题,也可以对一个组的上限值采用小数点的形式,小数点的位数根据所要求的精度来确定。
统计表的设计
统计表一般由四个主要部分组成,即
- 表头:一般应包括表号、总标题和表中数据的单位等内容。如果表中的全部数据都是同一计量单位,可在表中的右上角标明,若各单位的计量单位不同,则应在每个变量后或单列一列标明。
- 行标题:行标题之间通常不用横线隔开
- 列标题:列标题之间在必要时可用竖线分开,表中的上下两条横线一般用粗线,中间的其他线用细线。
- 数据资料:
统计表左右两边不封口。表中的数据一般是右对齐,有小数点时应以小数点对齐,小数点位数应统一。对于没有数据的表格单元,一般用“-”表示,一张填好的统计表不应出现空白单元格。
必要时可以在统计表的下方加上表外附加。表外附加通常放在统计表的下方,主要包括数据来源、变量的注释和必要的说明。